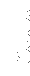CHAPITRE 10INSTRUCTIONS EXTERNES ET EXTENSIONS GRAPHIQUES Ce chapitre explique comment des instructions supplémentaires peuvent être ajoutées à celles déjà connues du BASIC. Par exemple, une Instruction dessinant des cercles sera ajoutée au BASIC d'Amstrad. Ces programmes seront entièrement écrits en langage assembleur et Interfaces avec l'interpréteur BASIC en utilisant des instructions externes. Ce chapitre utilise certaines des propriétés les plus avancées de l'assembleur. Il est recommandé de lire d'abord l'annexe 6. INSTRUCTION EXTERNE (RSX) Toutes les instructions du BASIC (LIST, GOTO, RND etc.) sont dites "instructions internes". Quand un programme BASIC est exécuté et que l'interpréteur rencontre une instruction interne il la recherche dans la ROM (Read Only Memory = mémoire de lecture uniquement) tandis que, si une instruction externe est rencontrée, il recherche aussi dans la RAM (mémoire de lecture/écriture). Une instruction externe ou extension du système résident (RSX) est une chaîne de caractères alphanumériques précédée d'une barre verticale (Shift et @). Voici les instructions externes légales: ùCIRCLE ùTRIANGLE ùBOX Essayez de taper ùBOX en BASIC. L'ordinateur répondra par "Unknown command". Cela parce que l'interpréteur ne peut trouver l'instruction BOX en ROM ni en RAM, Il est assez simple de dire à l'ordinateur qu'une Instruction externe existe; voici comment: Phase 1 L'ordinateur a d'abord besoin de savoir que des instructions externes vont être ajoutées. On accomplit cela en créant une table d'instructions nouvelles. Cette table d'Instructions agit comme un bloc de sauts à des tables supplémentaires, apportant des informations explicites sur les nouvelles instructions, c'est-à-dire syntaxe, emplacement etc. Ces informations sont transmises au système d'exploitation, en appelant un sous-programme en ROM, après avoir chargé dans les registres appropriés les données et l'adresse d'un buffer de quatre octets requis par le système d'exploitation. Utilité de la routine: Fait enregistrer une commande externe par le système d'exploitation (c'est-à-dire dit au système que l'instruction existe. Adresse d'appel: &BCD1 Conditions d'entrée: BC= adresse mémoire de départ de la table d'instructions externes HL= adresse mémoire de départ du buffer de quatre octets. Maintenant, toute cette procédure va être illustrée par un exemple. La table d'instructions externes commencera a l'adresse mémoire représentée par l'étiquette EXCOMT (EXternal COMmand Table). La méthode la plus facile pour réserver quatre octet pour un buffer est d'utiliser la directive d'assembleur "DEFA". On affectera à ce buffer le label BUFF: Donc:- BUFF: DEFS &04 En combinant ces différents éléments: PROGRAMME 10.1(ne pas entrer tout de suite) BUFF: DEFS &04 ;Installe buffer LD BC,EXCOMT: BC=départ de table LD HL,BUFF: ;HL=départ de buffer CALL &BCD1 ;Table d'enregistrement RET ; Retour au BASIC. N'entrez pas ce programme tout de suite car comme l'ordinateur connaît l'emplacement de la table d'instructions externes il ne trouverait pas de nom d'instruction nouvelle en la parcourant, Dès lors la table d'instructions externes nouvelles doit être remplie avec des noms d'instruction nouveaux. Phase 2 Des détails supplémentaires sur la table d'instructions nouvelles doivent figurer dans une table additionnelle. L'adresse de cette table est donnée par l'étiquette NENAM (NEw NAMe). La première ligne de cette section est donc:- EXCOMT: DEFW NENAM: On ajoute alors les nouveaux noms d'instruction en utilisant les instructions JP comme suit. JP BOX: Cela affectera une adresse de saut à la nouvelle instruction BOX. En admettant qu'une seule instruction externe va être ajoutée, la deuxième partie du programme apparaît comme ci-dessous: EXCOMT: DEFW NENAM: JP BOX: Maintenant, tout ce dont on a besoin est d'ajouter les caractéristiques du nom de la nouvelle instruction. Phase 3 Le nom de la nouvelle instruction est entré comme une chaîne de caractères ASCII en commençant par l'adresse mémoire désignée par NENAM. Le système d'exploitation de l'Amstrad a besoin que le bit 7 soit mis dans l'octet représentant le dernier caractère ASCII de la chaîne du nom de l'instruction. Il est très facile d'accomplir cela en ajoutant 880 au code ASCII de la dernière lettre, Dès lors, dans l'exemple, &80 doit être ajouté à l'ASCII de "X". Cette partie du programme se présente donc comme ci-dessous: NENAM: DEFM "BO" DEFB "X"+880 DEFB 80 Le 80 indique la fin de la table. Combiner ces trois parties ensembles: PROGRAMME 10.2 (ne pas assembler tout de suite) ORG 40000 BUFF: DEFS &04 LD BC,EXCOMT: LD HL,BUFF: CALL &BCD1 RET EXCOMT: DEFW NENAM : JP BOX: NENAM: &emspDEFM "BO" DEFB "X"+&80 DEFB 80 Notez que ORG a été mis sur 40000. En mettant alors MEMORY sur 39999, empêchant ainsi le BASIC d'utiliser une case mémoire au-dessus de 39999, l'instruction externe ne peut être altérée. Quand on tapera ùBOX, a partir du BASIC, l'ordinateur sautera à la case mémoire adressée par l'étiquette BOX. Pour illustrer la nouvelle instruction externe tapez le Programme 10.3 immédiatement après le programme 10.2. PROGRAMME 10.3 BOX: LD A,66 CALL PRINT: LD A,79 CALL PRINT: LD A,88 CALL PRINT: RET PRINT: EQU &BB5A Remarquez l'utilisation de l'étiquette mémoire PRINT Maintenant assemblez le programme entier; une fois listé il apparaîtra comme ci-dessous. ORG 10000 BUFF: DEFS 804 LD BC,EXCOMT: LD HL,BUFF: CALL &BCD1 RET EXCOMT: DEFW NENAM: JP BOX: NENAM: &emspDEFN "BO" DEFB "X"+&80 DEFB &0 BOX: LD A,66 CALL PRINT: LD A,79 CALL PRINT: LD A,88 CALL PRINT: RET PRINT: EQU &BB5A Exécutez le programme avec un 'CALL 40000' à partir du BASIC. Bien que rien de visible ne se soit produit, l'instruction externe BOX a été prise en charge Par le système d'exploitation de l'Amstrad. Revenez en BASIC et tapez: ùBOX BOX apparaît sur l'écran! Tout programme en langage assembleur adressé avec l'étiquette BOX peut donc être appelé avec cette instruction externe. On peut par exemple dessiner un rectangle sur l'écran, en utilisant les sous-programmes de graphisme intégrés. Pour préciser la taille du rectangle. Il faut transmettre certains paramètres à l'assembleur. Considérons le diagramme suivant: 
FIGURE 10.1
En définissant deux angles opposés diagonalement, on peut décrire un rectangle unique. Il serait utile si, de même que la taille, on pouvait changer la couleur du rectangle. C'est donc cinq paramètres qu'il faut transmettre au sous-programme en langage assembleur. Une solution envisageable serait d'écrire les données dans un bloc de mémoire, créant un "bloc de données". Bien qu'encombrant, cela marcherait. Heureusement, le système d'instructions externes crée ce bloc de données pour nous, Quand elle est appelée, la case de départ du bloc de données est stockée dans le couple de registres IX, et le nombre d'éléments de données est stocké dans l'accumulateur. Considérons l'instruction suivante qui dessinera un rectangle de 100 Par 100 unités sur l'écran en 200,100 avec ink 2 ùBOX, 200,100,300,200,2 
FIGURE 10.2 Les paramètres du rectangle sont convertis en hexadécimal avant d'être stockés en mémoire. Phase 1 100 = &0064 200 = &00C8 300 = &012C 2 = &0002 Phase 2 Les paramètres sont stockés avec l'octet faible en premier suivi immédiatement par l'octet fort. Le dernier paramètre entré est désigné par IX, les paramètres de l'exemple sont donc stockés comme suit: Case ; Contenu mémoire ; Hex Décimal IX+0 ;02 2 IX+1 ;00 IX+2 ;00 200 IX+3 ;C8 IX+4 ;01 300 IX+5 ;2C IX+6 ;00 100 IX+7 ;64 IX+8 ;00 200 IX+9 ; C8 En utilisant un décalage approprié on peut avoir accès a n'importe lequel de ces paramètres. Remarquez que chaque paramètre est stocké sur deux octets, un paramètre peut se trouver dans l'intervalle 0-65535. Maintenant, des coordonnées transmises par l'instruction externe, quatre couples de coordonnées doivent être dérivées pour décrire le rectangle. Considérons la Figure 10.3: 
FIGURE 10.3 Comme les coordonnées X,Y et X1,Y1 sont transmises par l'Instruction externe on doit en déduire les coordonnées des deux autres angles et tracer le rectangle. Ceci est représenté par l'organigramme suivant: 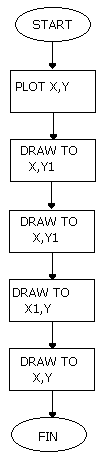
FIGURE 10.4 Exprimons cet organigramme dans un programme (remarquez l'utilisation de la Pile pour stocker les coordonnées): PROGRAMME 10.4 10 DRAW: EQU &BBF6
20 PLOT: EQU &BBEA
30 INK : EQU &BBDE
40 BOX: LD A,(IX+0)
50 CALL INK:
60 LD D,(IX+8)
70 LD D,(IX+9)
80 PUSH DE
90 LD E,(IX+6)
100 LD D,(IX+7)
110 PUSH DE
120 LD E,(IX+4)
130 LD D,(IX+5)
140 PUSH DE
150 LD E,(IX+2)
160 LD D,(IX+3)
170 PUSH DE
180 LD E,(IX+8)
190 LD D,(IX+9)
200 LD E,(IX+6)
210 LD H,(IX+7)
220 PUSH DE
230 CALL PLOT:
240 POP DE
250 POP HL
260 PUSH HL
270 CALL DRAW:
280 POP HL
290 POP DE
300 PUSH DE
310 CALL DRAW:
320 POP DE
330 POP HL
340 PUSH HL
350 CALL DRAW:
360 POP HL
370 POP DE
380 CALL DRAW:
390 RETL'utilisation des étiquettes pour les adresses de mémoire augmente grandement la lisibilité du programme. Maintenant remplacez le sous-programme commençant avec l'étiquette BOX dans le programme précédent par le programme 10.4.Assemblez-le et exécutez-le. Maintenant revenez en BASIC et essayez le programme 10.5, après avoir intégré l'instruction avec un "CALL 40000". Remarque: Comme l'assembleur utilise les lignes BASIC au-dessus de 64000, ne tapez pas NEW ou vous devrez recharger l'assembleur. PROGRAMME 10.5 10 MODE O:CALL 40000
20 X=RND(1)*550
30 Y=RND(1)*350
40 X1=RND(1)*50
50 Y1=RND(1)*50
60 C=RND(1)*15
70 ùBOX,X,Y,X+X1,Y+Y1,C
80 GOTO 20Ceci conclut la partie sur les instructions externes. Le reste de ce chapitre expliquera comment on peut ajouter des instructions graphiques additionnelles.QUELQUES INSTRUCTIONS GRAPHIQUES SUPPLEMENTAIRES 1.BOX,X,Y,X1,Y1,C Dessine un rectangle sur l'écran en utilisant le PEN C 2. BOXF,X,Y,X1,Y1,C où les arguments sont exactement les mêmes que pour BOX. La seule différence est que le rectangle est plein. 3. TRI,X,,Y,X1,Y1,X2,Y2,C Dessine un triangle sur l'écran. Avec: 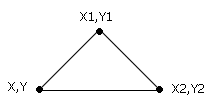
Notez que Y doit être égal à Y2 4. CIRCLE,X,Y,R,C Avec: 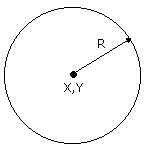
Les instructions externes résident en mémoire en commençant à la case mémoire 40000. Pour s'assurer qu'elles ne soient pas altérées on ramène le pointeur de mémoire BASIC sur 39999 avec l'instruction suivante: MEMORY 39999 Il est donc sage de s'assurer que les deux premières lignes de programme BASIC utilisant ces instructions sont les suivantes: 1 MEMORY 39999 2 CALL 40000 : Les instructions de remplissage du rectangle Ces instructions dessinent un rectangle plein sur l'écran; il est dessiné comme une série de lignes horizontales consécutives. Considérons la figure 10.5 
FIGURE 10.5 L'algorithme pour remplir ce rectangle se présente ainsi: 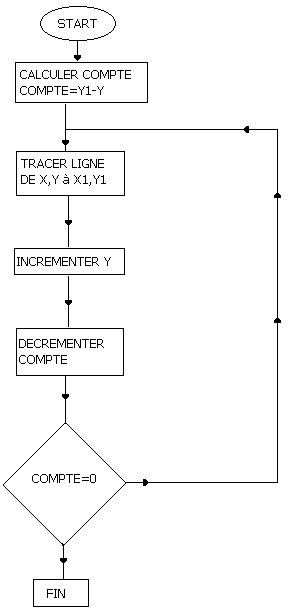
FIGURE 10.6 Exprimons cet algorithme dans un programme PROGRAMME 10.6 10 COUNT: DEFS 4
20 DRAW: EQU &BBF6
30 PLOT: EQU &BBEA
40 INK: EQU &BBDE
50 BOXF: LD A,(IX+0)
60 CALL INK:
70 LD L,(IX+2)
80 LD H,(IX+3)
90 LD E,(IX+6)
100 LD D,(IX+7)
110 AND A
120 SBC HL,DE
130 JP C,END:
140 LD (COUNT:),HL
150 LD E,(IX+8)
160 LD D,(IX+9)
170 LD L,(IX+6)
180 LD H,(IX+7)
190 PUSH HL
200 PUSH DE
210 CALL PLOT:
220 LD E,(IX+4)
230 LD D,(IX+5)
240 POP IX
250 POP IY
260 NXT: PUSH DE
270 PUSH IY
280 POP HL
290 CALL DRAW:
300 PUSH IX
310 POP DE
320 POP IX
330 INC IY
340 LD HL,(COUNT:)
350 PUSH DE
360 LD DE,1
370 AND A
380 SBC HL,DE
390 LD (COUNT:),HL
400 POP DE
410 JR NZ,NXT:
420 END: RETLa cassette d'assembleur (face B) contient un fichier appelé GRAPHICS-EXT qui contient toutes les instructions graphiques additionnelles présentées dans ce chapitre, Pour l'utiliser chargez l'assembleur puis chargez le fichier GRAPHICS-EXT et assemblez-le. Si vous désirez utiliser une instruction supplémentaire dans vos programmes BASIC, sauvegardez une copie du code objet produit en utilisant l'identificateur de fichier '-b'. Sauvegardez-la par exemple sous le nom GRAPHICS-B, Ce fichier peut alors être chargé a partir du BASIC avec l'instruction : LOAD "GRAPHICS-B",40000.Assurez-vous cependant que le pointeur de mémoire BASIC a d'abord été ramené sur 39999, en utilisant a la suite l'instruction MEMORY 39999. Ensuite pour intégrer les instructions graphiques, tapez CALL 40000 à partir du BASIC. Maintenant toutes les instructions sont disponibles. Etudiez le programme de présentation des instructions supplémentaires GRAPHICS-DEMO si vous n'êtes pas sûr de vous. L'INSTRUCTION TRIANGLE Cette instruction produit un triangle plein sur l'écran. La méthode utilisée est itérative et est choisie pour sa simplicité plutôt que son efficacité. Dans cette méthode une procédure donnée est répétée jusqu'à ce qu'une condition soit remplie. Ici la différence entre deux coordonnées de la base X est utilisée comme compteur. Voir la figure 10.7 
FIGURE 10.7 Une série de lignes sont dessinées du sommet (X1,Y1) à la base. Cela se traduit par le fait que le pixel (point) du sommet est réécrit un nombre de fois égal au compteur. Les pixels à proximité du sommet sont aussi réécrits, mais moins fréquemment. C'est un algorithme très peu efficace; l'idéal serait que chaque pixel du triangle soit écrit une fois. Cela peut être accompli en utilisant des algorithmes plus complexes (par exemple un algorithme scan-line), Mais ceci dépasse le cadre de ce livre. Voici le listing de l'instruction triangle: 10 COUNT: &emspDEFS 4
20 DRAW: EQLI &BBF6
30 PLOT: EQU &BBEA
40 INK: EQU &BBDE
50 TPI: LD A,(IX+0)
60 CALL INK:
70 LD E,(IX+12)
80 LD D,(IX+13)
90 LD L,(IX+4)
100 LD H,(IX+5)
110 AND A
120 SBC HL,DE
130 JP M,END:
140 LD (COUNT:),HL
150 LD E,(IX+8)
160 LD D,(IX+9)
170 LD L,(IX+6)
130 LD H,(IX+7)
190 PUSH DE
200 PUSH HL
210 LD L,(IX+10)
220 LD H,(IX+11)
230 PUSH HL
240 POP IY
250 POP IY
260 LD E,(IX+12)
270 LD D,(IX+13)
230 PUSH DE
290 POP IX
300 NXTT: POP HL
310 POP DE
320 PUSH DE
330 PUSH HL
340 CALL PLOT:
350 PUSH IX
360 POP DE
370 PUSH IY
330 POP HL
390 CALL DRAW:
400 INC IX
410 LD HL,(COUNT:)
420 LD DE,1
430 AND A
440 SBC HL,DE
450 LD (COUNT:),HL
460 JR NZ,NXTT:
470 POP DE
4S0 POP DE
490 END: RET L'instruction CIRCLE La méthode la plus simple pour réaliser un cercle sur l'écran utilise les fonctions SIN et COS de l'Amstrad. Considérons la figure 10.8: 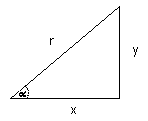
FIGURE 10.8 En incrémentant dans l'intervalle 0<alpha<pi/2 et en fixant un point aux coordonnées (X,Y) on obtient un quart de cercle. Ce quart peut être développé en un cercle plein. En admettant que le centre du cercle est le point d'origine du graphique, considérons la figure 10,9 pour le point X,Y. 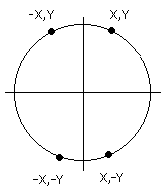
FIGURE 10.9 Même si cette méthode fonctionne, elle est pratiquement inefficace parce que les fonctions SIN et COS nécessitent un temps de calcul considérable qui ralentit l'algorithme. Un algorithme légèrement plus efficace peut-être dérivé du théorème de Pythagore, équation 10.1 ci-dessous: Théorème de Pythagore 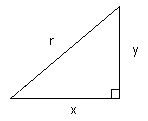
R^2 = X^2 + Y^2 ;Equ 10.1 Réajustons l'équation 10.1: Pour dessiner un quart de cercle comme auparavant, X doit être incrémenté dans l'intervalle 0<=X<=R, on trouve alors le Y correspondant à chaque valeur de X, et le Pixel de coordonnées X,Y est mis. Essayez le programme BASIC suivant: PROGRAMME 10.8 10 MODE 0
20 DEFINTx,y,r
30 x=0
40 r=100
50 WHILE X<r
60 y=SQR(r*r-x*x)
70 PLOT x,y
80 x=x+1
90 WEND
100 END Ce programme réalise un quart de cercle comme ci-dessous dans la figure 10.10 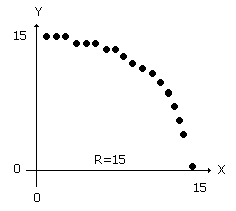
FIGURE 10.10 Il y a deux limites principales à l'utilisation de cette méthode. 1. La qualité de l'arc laisse à désirer à mesure que X s'approche de R. 2. Bien que plus rapide que SIN ou COS, la recherche de la racine carrée d'un nombre demande quand même un temps de calcul considérable. Il y a différentes méthodes qui permettent d'amoindrir ces problèmes. Dans ce chapitre nous nous attarderons sur une solution possible. Elle est basée sur l'algorithme de Bresenham développé à l'origine pour les traceurs mécaniques. Cet algorithme est considérablement plus efficace que toutes les méthodes mentionnées précédemment car toutes les opérations arithmétiques peuvent être accomplies facilement grâce à quelques additions, soustractions et décalages.
UNE ADAPTATION DE L'ALGORITHME DE BRESENHAM POUR DESSINER LES CERCLES Au lieu d'incrémenter X dans l'intervalle 0<=X<=R cette méthode utilise l'intervalle 0<=X<=pi/4 produisant donc un segment à 45 degrés. On obtient le cercle complet en réfléchissant les points calculés. Le Cœur de l'algorithme est un sous-programme qui sélectionne le pixel le plus proche du cercle véritable au point considéré. La distance entre le cercle véritable et le pixel sélectionné est appelée "terne d'erreur" et est déduite de la manière suivante:- Utilisons le théorème de Pythagore R^2 = x^2 + y^2 admettons que le pixel est fixé en X,Y, le terme d'erreur est alors donné par E= (x^2+y)-r^2 En diminuant E à chaque phase, on obtient l'approximation d'un cercle la plus proche possible sur une grille de pixels discontinue. 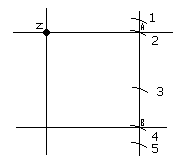
FIGURE 10.11 Si on admet que le pixel noir Z vient d'être mis, le prochain pixel à "être mis sera soit A, soit B. Si on définit le terme d'erreur comme étant la différence entre le carré des distances du centre du cercle aux pixels A ou B et au cercle actuel à ce point, on peut calculer les équations suivantes. Pour Pixel A E =(x^2+y^2)-r^2 ;Equ 10,2 Pour pixel B E =(x^2-y^2)-r^2 ;Equ 10.3 Donc si la valeur absolue de E de A est supérieure ou égale à la valeur absolue de E de B, c'est le pixel B qui est mis et si la valeur absolue de E de A est inférieure à la valeur absolue de E de B, c'est le pixel A qui sera mis. Combinons les équations 10.2 et 10.3 pour former le terme d'erreur totale E: E = E + E T A B Maintenant si E >=0, le pixel B est mis, sinon E ; T ; T Reconsidérons la figure 10.11 Case 1 E T Case 2 E T Case 3 E T Case 4 E >=0 le pixel B est mis T Case 5 E >=0 le pixel B est mis T Comme on peut le voir la méthode fonctionne, cependant il est quand même nécessaire de calculer le carré et la racine carré des données pour calculer le terme d'erreur. Grâce a une série d'opérations arithmétiques, on peut montrer que l'erreur initiale se présente ainsi:
E = 3-2r ;Equ 10.4 T La valeur de E(T) change tout au long du programme suivant le choix du pixel précédent: Si le Pixel A est choisi quand E ; T ;T E = E +4X+6 ; Equ 10.5 T+1 T ou si le pixel B est sélectionné quand E >=0 alors ;T E = E +4(x-y)+10 ; Equ 10.7 T+1 T L'équation 10,5 a besoin de deux additions et deux décalages, l'équation 10.6 de deux additions, une soustraction et deux décalages; un progrès considérable sur les algorithmes précédents. On a besoin d'une méthode pour réfléchir ces points afin de former un cercle complet. Si on peut trouver les valeurs de X et Y pour un quart de cercle, on peut alors produire un cercle complet en réfléchissant ces coordonnées. Voir figure 10.12 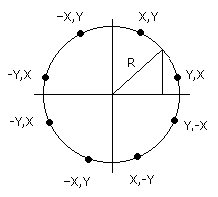
FIGURE 10.12 Cet algorithme est démontré dans le programme BASIC suivant: PROGRAMME 10.9 10 MODE 1 20 radius=100 30 x=0 40 y=radius 50 origin 320,200 60 diff=3-2*radius 70 while x<y 80 gosub 50 90 if d100 d=d+4*(x-y)+10 110 y=y-1 120 x=x+1 130 wend 140 end 150 plot x,y 160 plot y,x 170 plot y,-x 180 plot x,-y 190 plot x,-y 200 plot -x,-y 210 plot -y,-x 220 plot -y,x 230 plot -x,y 240 return Le programme produit une distribution des pixels comme dans la figure 10.13, pour un rayon de 15. 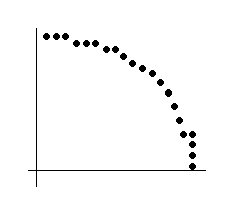
FIGURE 10.13 Ici l'algorithme est converti en langage assembleur: Pour économiser vos doigts, toutes les instructions externes sont incluses dans la cassette sous le nom de GRAPHICS-EXT. PROGRAMME 10.10 10 PLOT: EQU &BBEA 20 INK: EQU &B6DE 30 ORGIN: EQU SBBCC 40 ORGET: EQU &BBCC 50 DIFF: DEFS 2 60 RAD: DEFS 2 70 X: &emspDEFS 2 80 Y: &emspDEFS 2 90 XO: DEFS 2 100 YO: DEFS 2 ne CIRCLE: CALL ORGET: 120 LD(XO:),DE 130 LD A,(IX+0) 140 CALL INK: 150 LD (YO:),HL 160 LD D,(IX+7) 170 LD E ,(IX+6) 180 LD H,(IX+5) 190 LD L,(IX+4) 200 PUSH HL 210 LD H,(IX+3) 220 LD L,(IX+0} 230 LD (RAD:),HL 240 POP HL 250 CALL ORGIN: 260 LD BC,0000 270 LD (X:),BC 2S0 LD HL,(RAD:) 290 LD (Y:),HL 300 SLA L 310 RL H 320 PUSH HL 330 POP DE 340 LD HL,3 350 XOR A 360 SBC HL,DE 370 LD (DIFF),HL 380 CALC: LD HL,(X:) 390 LD DE,(Y:) 400 PUSH HL 410 PUSH DE 420 CALL MIRIM: 430 POP DE 440 POP HL 450 XOR A 460 SBC HL,DE 470 JP P,END2: 430 LD HL,(DIFF:) 490 LD BC,0000 500 SBC HL,BC 510 JP P,LESS: 520 LD DE,(X:) 530 SLA E 540 RL D 550 SLA E 560 RL D 570 LD HL,6 530 ADD HL,DE 590 LD DE,(DIFF:) 600 ADD HL,DE 610 JP NXT3: 620 LESS: LD HL,(IX:) 630 LD DE,(Y:) 640 XOR A 650 SBC HL,DE 660 SLA L 670 RL H 680 SLA L 690 RL H 700 LD DE, 10 710 ADD HL,DE 720 LD DE,(DIFF:) 730 ADD HL,DE 740 LD DE,(Y:) 750 DEC DE 760 LD (Y:),DE 770 NXT3: LD (DIFF:),HL 780 LD HL,(X:) 790 INC HL 800 LD (X:),HL 810 JP CALC: 820 MIRIM: LD DE,(X:) 830 LD HL,(Y:) 840 CALL PLOT: 850 LD DE,(Y:) 860 LD HL,(X:) 870 CALL PLOT: 880 LD HL,0000 890 LD BC,(X:) 900 XORA 910 SBC HL,DE 920 PUSH HL 930 PUSH HL 940 LD DE,(Y:) 950 CALL PLOT: 960 POP DE 970 LD HL,(Y:) 930 CALL PLOT: 990 LD HL,0000 1000 LD BC,(Y:) 1010 XOR A 1020 SBC HL,BC 1030 PUSH HL 1040 PUSH HL 1050 LD DE,(X:) 1060 CALL PLOT: 1070 POP DE 1080 LD HL,(X:) 1090 CALL PLOT: 1100 POP HL 1110 POP DE 1120 PUSH HL 1130 PUSH DE 1140 CALL PLOT: 1150 POP HL 1160 POP DE 1170 CALL PLOT: 1180 RET 1190 END2: LD DE,(X0:) 1200 LD HL,(Y0:) 1210 CALL ORIGIN: 1220 RET Ça y'est, vous y êtes arrivé. Bien Joué. Nous espérons que le livre vous a plu et que sa lecture vous a été profitable. Joyeuse programmation !
CPCrulez[Content Management System] v8.732-desktop
Page créée en 437 millisecondes et consultée 1906 foisL'Amstrad CPC est une machine 8 bits à base d'un Z80 à 4MHz. Le premier de la gamme fut le CPC 464 en 1984, équipé d'un lecteur de cassettes intégré il se plaçait en concurrent du Commodore C64 beaucoup plus compliqué à utiliser et plus cher. Ce fut un réel succès et sorti cette même années le CPC 664 équipé d'un lecteur de disquettes trois pouces intégré. Sa vie fut de courte durée puisqu'en 1985 il fut remplacé par le CPC 6128 qui était plus compact, plus soigné et surtout qui avait 128Ko de RAM au lieu de 64Ko. |
|